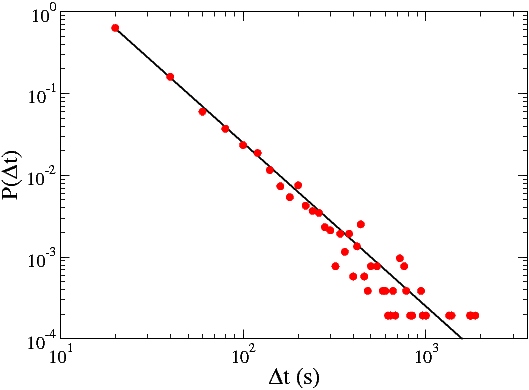
Contact durationWe just completed a first experiment with our new contact-detection firmware for the OpenBeacon platform. The experiment was hosted at a conference on “Facing the Challenge of Infectious Diseases” and involved about 50 attendees over four days. The new firmware proved to be as much reliable in a real-world setting as it appeared to be in our preliminary experiments. In the next posts, we will report on different aspects of this new experiment. As a first example of hidden patterns in the dynamics of social contacts, we display below the probability of observing a face-to-face contact of a given duration. The probability P(Dt) of observing a contact of duration Dt is shown as a function of the contact duration Dt. The probability distribution was computed using a few hours of data. The interval of time we analyzed was divided into slices of 20 seconds, and for each of these slices the contact graph of the attendees was computed and used to assess when a new contact was established, continued, or broken. As a consequence, the contact durations we measure are multiples of the interval used for temporal coarse-graining (i.e., contacts last 20 seconds, 40 s, 60 s, …) Remarkably, this simple analysis exposes a clear pattern of social contact: the duration of face-to-face contacts is power-law distributed (straight line on a log-log plot) with an exponent close to -2 (black line). This behavior holds over different periods of time, and is robust across different groups of individuals. Qualitatively, the figure above shows something obvious: there are comparatively few long-lasting contacts and a multitude of brief contacts. It is remarkable, however, that such a clear-cut pattern emerges when observing a few tens of persons over a few hours. Moreover, the specific value of the scaling exponent (-2) shows that the duration of social contact is scale-free, i.e., there is no “typical” duration for contacts. While one can always compute an average duration of contacts over a finite sample of data, the scaling properties are such that the computed average will increase without limit on increasing the length of the experiment. We close by noticing that we are not the first to observe this regularity for the duration of social contacts (see for example the work by Scherrer et al. on “Description and simulation of dynamic mobility networks”). Our measurements, however, achieve higher spatial and temporal accuracy than previous studies, and reliably select face-to-face interactions at close range, which are a very good proxy for social interaction. |
|
![SocioPatterns [logo]](http://www.sociopatterns.org/wp-content/themes/sp2/images/header_logo.png)